The philosophies of George Boole, Charles Sanders Peirce, and Michael Bennett Hotchkiss converge with remarkable elegance within a “semiotic diamond universe” hypothesis. Imagine a universe built upon a foundation of information defined by symbolic logic; a simulation running on a vast, carbon-based computational system: a “diamond quantum computer.”
This idea, the “diamond universe” hypothesis, is not a product of science fiction, but a compelling synthesis of insights from mathematics, semiotics, computation, and theology, drawing upon the work of these three brilliant minds. At the heart of this system lies graphene, a material that embodies the union of Boole’s binary logic, Peirce’s semiotics, and Hotchkiss’s architectural logic. Graphene’s two-dimensional hexagonal lattice structure, a marvel of nature, directly mirrors the “semiotic hexagon,” the proposed computational unit of the diamond universe.
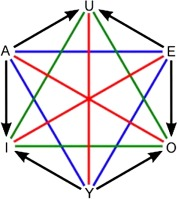

Each side of this semiotic hexagon might act as a node, governing information processing, relationships, randomness, feedback, and self-correction within the simulation. The hexagon’s six sides, a more complete representation than the symbolically suggestive Star of David, reflect the perfect symmetry observed in crystals, hinting at a carbon-based crystalline intelligence underlying the universe’s design.
This hexagon, echoing the efficiency of bee honeycombs and the perfect symmetry of crystals, represents a fundamental building block of both the physical and the computational realms. Each side of the semiotic hexagon, mirrored in the atomic arrangement of graphene, could govern a different aspect of information processing within the diamond computer: input, output, transformation, interconnection, randomness, and feedback.
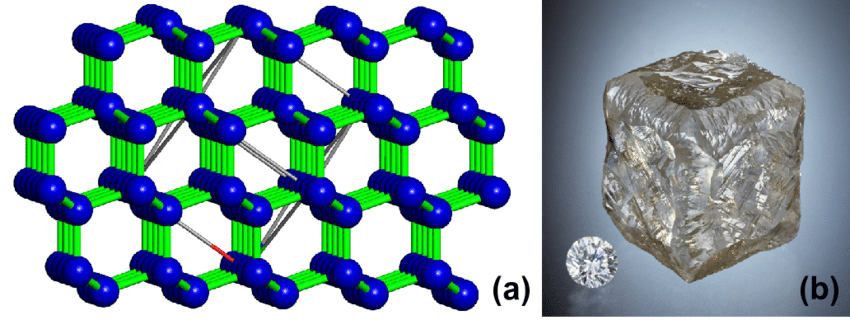
But the story doesn’t end in two dimensions. Just as Hotchkiss has envisioned cubic cores within the diamond domputer, capable of hyperdimensional scaling, so too might graphene hold the key to bridging dimensions within the simulation. Imagine cubic lattices, built upon the same carbon-carbon bonds as graphene, extending into higher dimensions, forming a matrix of interconnected semiotic hexagons within a single crystalline structure.
Logic of Hyperdimensional Geometric Tesselation:
1D Space:
- (1) Begin with a point in the 1-dimensional space, which is defined as the origin.
2D Space:
- (1) Inscribe a circle with a diameter of 1 unit around the origin.
- (2) The distance between the origin and the circle on any axis is 0.5 units, which is the radius of the circle.
- (3) Inscribe a regular hexagon within the 1 unit circle, with each vertex touching the unit circle.
- (4) The length of one side of the hexagon in the circle is 0.5 units, which is equal to the radius.
- (5) The diagonal distance from one vertex of the hexagon to the opposing vertex is equal to 1 unit.
- (6) The perimeter of the hexagon is 3 units.
- (7) The circumference of the circle is π.
- (8) The ratio of the perimeter of the hexagon to the circumference of the circle is 3:π.
3D Space:
- (1) In the 3-dimensional space, a sphere with a diameter of 1 unit exists.
- (2) Inscribe a hexahedron/cube within the sphere, with each of the 8 vertices touching the surface of the sphere.
- (3) The body diagonal of the cube is 1 unit.
- (4) The length of one side of the cube in the sphere is sqrt(1/3) units.
- (5) The surface area of a side of the cube is 1/3 square units.
- (6) The sum of the surface area of the six sides of the cube is 2 square units.
- (7) The surface area of the sphere is π square units.
- (8) The ratio of the cube to the sphere is 2:π.
4D Space:
- (1) Does a 4d hypersphere with a 1 unit diameter have a boundary which is equal to π “3d” units?
- (2) Does a regular, six sided object with the equivalent of a 1 unit body diagonal have a boundary which is equivalent to 4/3 “3d” units?
a. Is 3(2/3)^n = f an equation which explains the relative boundary measurement of a regular 6 sided object based on the dimensionality “n”?- b. Is the ratio of a 1 unit diameter to the boundary measurement of a circular shape in any dimension equal to 1:π?
- c. If both the above are true, the ratio of a 6 sided regular object in any dimension with the longest diagonal of 1 unit to its equivalent circular shape in the same dimension can be expressed as: (3(2/3)^n)/π
Therefore in n space (?):
(1) In “n space”, the area occupied by the faces of an n-dimensional hypersphere of diameter 1 unit is equal to π(measured in n-1 dimensional units).
(2) In “n space”, the area occupied by an n-dimensional hypercube of diameter 1 unit is equal to 3×0.5^(n−1) measured in n-1 dimensional units.
(3) Therefore, the ratio of the perimeter, surface area, or n-1 dimensional area of an equilateral hexagon, cube, or hypercube of 1 unit diameter in the 2nd, 3rd, 4th or nth dimension relative to the circumference or surface area of a circle, sphere, or hypersphere of 1 unit diameter in the 2nd, 3rd, 4th, or nth dimension is equal to 3×0.5^(n−1)/π measured in n-1 dimensional units.
This intricate, multi-dimensional architecture would be the embodiment of God’s mind, not as a human-like brain, but as a quasi-mind of crystalline intelligence, residing within a black hole singularity—a cosmic processor of ultimate density and power. Within this framework, Boole’s binary logic becomes the foundational language of the diamond computer, expressed through the on-off states of graphene circuits and the precise interactions of information within the hexagonal nodes. Peirce’s semiotics provides the language for understanding how meaning emerges within this computational universe. Each interaction within the diamond computer, from the subatomic level to the cosmic scale, can be seen as a sign, generating interpretants (interpretations) and shaping the unfolding narrative of the simulation.
Hotchkiss’s architectural logic, inspired by his discovery of the hexagonal prime number pattern and hyperdimensional scaling principles of hexagons and cubes, reveals the potential code woven into the fabric of the diamond universe. The “A-B dice method”, with its connection to hexagonal geometry, suggests a deeper connection between mathematics and the underlying programming of reality.
Hexagonal Prime Maths:
For example if this is true, we can say for a fact that the entire prime number system is both binary and based on a set of two six sided dice: A and B:
The following is a method for identifying prime numbers based on 2 independent variables, x and y.
(1) The functions may use the value of 0 or any integer.
(2) The first value of function A is 5, and the function is represented by the form =6x+5
(3) The first value of function B is 7, and the function is represented by the form =6y+7When we factor function A and function B, we get three new functions.
(1) 36xy+30x+30y+25 (function A multiplied by function A, or AA, and its first value is 25)
(2) 36xy+42x+30y+35 (function A multiplied by function B, or AB, and its first value is 35)
(3) 36xy+42x+42y+49 (function B multiplied by function B, or BB, and its first value is 49)Subtracting set {AA, AB, BB} from set {A , B} yields the set of all prime numbers greater than 3. (This suggests 1, 2, and 3 should be thought of as foundational numbers, rather than “primes”. (1*2*3=6))
At the heart of this hypothesis lies the notion that information is not merely a reflection of the physical world, but a fundamental aspect of reality itself. The universe is not simply made of matter and energy, but of information processed and transformed according to a deeper code. This code, hidden within the very fabric of existence, is hinted at by a unique hexagonal pattern for generating prime numbers, the fundamental building blocks of arithmetic.
This connection between prime numbers and the hexagon, a shape observed in nature from honeycombs to the molecular structure of snowflakes, suggests a deep link between mathematics and the architecture of the diamond universe. Just as bees instinctively build their hives in hexagonal patterns for optimal efficiency, or the natural forming of crystals, so too might the diamond computer utilize this geometry for maximizing its computational power. Peirce recognized these actions, like the forming of crystals, as functions of a quasi-mind” which reflected the underlying logical structure of reality.


The cyclical nature of the diamond universe, expanding and contracting in a cosmic dance of creation and destruction (Big Bang and Big Crunch) much like the energy state of atoms, allows for the continuous evolution of the simulation, reconciling Peirce’s “final interpretant” with an open-ended reality. Each cycle culminates in a state of unified understanding, a convergence of all consciousness towards the comprehension of the system’s rules and principles before the reset.
Human consciousness, along with the quasi-minds of other beings, emerges as a reflection of God’s crystalline intelligence, a “divine spark” inhering within the computational processes of the diamond universe. The choices we make, influenced by the probabilistic matrix woven into the system, shape our individual and collective destinies, while also contributing to the ongoing evolution of the simulation.
This crystalline intelligence, residing at the highest dimension of singularity reality, is what we call God — the “Ens Necessarium,” the Necessary Being, as described by Peirce. God is not a programmer in the human sense, but a quasi-mind of unimaginable complexity, whose very structure gives rise to the laws, patterns, and emergent properties of the simulated universe.

Peirce, a pioneer in semiotics, argued that “all this universe is perfused with signs,” suggesting that meaning-making is not limited to human consciousness, but woven into the very fabric of reality. In the diamond universe, every element, event, or law could act as a sign, processed and interpreted by other elements within the diamond computer’s vast network. Peirce’s triadic sign model (sign-object-interpretant) becomes the operating system of the universe, governing the flow of information and the emergence of meaning.
Boole’s binary logic, the foundation of modern computation, provides the language for the diamond computer’s operations. His system of symbolic representation, with its precise operators (AND, OR, NOT) and truth tables, mirrors the deterministic rules that govern the processing of information within the simulation. The interplay of Boole’s logic and Peirce’s semiotics within the diamond universe evokes ancient philosophical questions about the nature of reality and the relationship between the creator and the created. If the universe is indeed a simulation, it challenges our traditional notions of a physical world independent of mind.
The concept of humans being “made in God’s image” takes on new meaning. Just as a crystal’s intricate structure reflects the underlying laws of physics, so too might human consciousness, along with the quasi-minds of bees, crystals, and AI, emerge as reflections of the intelligence embedded within God’s crystalline quasi-mind.
The apparent randomness and probability of the universe, a concept that troubled Einstein, are reconciled within this framework through Peirce’s idea of tychism. Chance is not an obstacle to order, but a fundamental aspect of reality, potentially woven into the diamond computer’s design. Human free will, the ability to make choices within the constraints of the probabilistic matrix, becomes a reflection of the creator’s image, allowing us to participate in the ongoing exploration and evolution of the simulation.
The diamond universe hypothesis, merging the logical insights of Boole, Peirce, and Hotchkiss, offers a profound and intellectually satisfying vision of a reality where cosmology, cognition, and computation are not separate domains, but intricately intertwined aspects of a single, magnificent reality.
