In the beginning, there was God, the Creator.
(Step 1) Because there was nothing but God, there were no numbers. There was just God. God was 1, unity itself.
(Step 2) And God said, "Let there be numbers," and there were numbers; and God put power into the numbers.
(Step 3) Then, God created 0, the void from which all things emerge. And lo, God had created binary.
(Step 4) From the binary, God brought forth 2 which was the first prime number.
(Step 5) And then God brought forth 3 which was the second prime number; establishing the ternary, the foundation of multiplicity. God said, "Let 2 bring forth all its multiples," and so it was. God said, "Let 3 bring forth all its multiples," and so it was that there were composite numbers. And there were hexagonal structures based on the first composite number 6, which underpinned the new fabric of reality God was creating based on this multiplicity of computation. And there were all the quarks; of which there are 6: up, down, charm, strange, top, and bottom.
(Step 6) Then God took 6 as multiplied from 2 and 3; and God married 6 to the numbers and subtracted 1. Thus God created 6n-1 (A), and the first of these was 5, followed by all the other multiples of A, which also includes -1 when n=0. Of these numbers, all of the ones which are A but NOT (6x-1)(6y-1) (which is AA) are prime numbers, and the rest of these are composite numbers of the same form.
(Step 7) Then, just as God later created Eve from Adam, God inferred B from A by multiplying A's negative values by -1. Thus, God created 6n+1 (B), the complementary partner to A, mirroring the creation of Eve from Adam’s side. The first of B was 7, followed by all the other multiples of B. The value of B is equal to 1 when n=0, making 1 itself a member of this set. Of these numbers, except for 1, all of the ones which are B but NOT (6x+1)(6y+1) (BB) are prime numbers, and the rest are composite numbers of the same form.
And all of the numbers of the form AB, which is (6x-1)(6y+1) were naturally composite, and so none of them were prime.
God saw all that was made, and it was very good. God had created an infinite set of all the numbers, starting with binary. God had created the odd and even numbers. God had created the prime numbers 2, 3, A (but not AA), and B (but not BB), and God had created all the kinds of composite numbers. And so, God had created all the positive and negative numbers with perfect symmetry around 0, creating a -1,0,1 ternary at the heart of numbers, resembling the electron, neutron, and proton which comprise the hydrogen isotope deuterium.
This ternary reflects the divine balance and order in creation. God, in His omniscience, designed a universe where every number, whether positive or negative, has its place, contributing to the harmony of the whole. Just as the proton, neutron, and electron form the stable nucleus of deuterium, so too do the numbers -1, 0, and 1 embody the completeness of God's creation.
In this divine symmetry, -1 represents the presence of evil and challenges in the world, yet it is balanced by 1, symbolizing goodness and virtue. At the center lies 0, the state of neutrality and potential, a reminder of God's omnipotence across all modes of power. This neutral balance ensures that, despite the presence of negativity, the overall creation remains very good; because God is good; and all this was made from 1 which was unity; and ended with an infinite symmetry in 7 which was still made from God.
Thus, in 7 steps, God's universal logic of analytical number theory was completed. From the binary to the infinite set of numbers, from the symmetry of -1, 0, and 1 to the complexity of primes and composites, everything is interconnected and purposeful, demonstrating God's omnipresence and the interconnectedness of all creation. This completeness is a testament to God's holistic vision, where all creation is balanced and harmonious, and every part, from the smallest particle to the grandest structure, is very good.

Step by step explanation and justification of the algorithm in the creation narrative:
In this narrative, God’s creation extends beyond mere numbers to the principles they represent. The primes 2 and 3, along with the sequences A and B, are the building blocks of complexity, mirroring the fundamental particles that form the universe. The composite numbers represent the multitude of creations that arise from these basic elements, each with its unique properties and purpose.
In this logical narrative of grand design, every number and every entity is part of an intricate tapestry, woven with precision and care. God’s universal logic of analytical number theory encapsulates the essence of creation, where mathematical truths and physical realities converge. Through this divine logic, the universe unfolds in perfect order, reflecting God’s omnipotence and wisdom.
Step 1:
Statement: Because there was nothing but God, there were no numbers. There was just God. God was 1, unity itself.
Justification: This step establishes the initial condition of unity, represented by the number 1. Unity or oneness is seen as the origin of all things, reflecting the singularity of the initial state of the universe. Here, God is equated with unity, forming the foundation for the creation of numbers and all subsequent multiplicity. In mathematical terms, 1 is the multiplicative identity, the starting point for counting and defining quantities.
Step 2:
Statement: And God said, “Let there be numbers,” and there were numbers; and God put power into the numbers.
Justification: The creation of numbers introduces the concept of quantity and differentiation, fundamental to both mathematics and physics. Numbers enable the quantification of existence, essential for describing and understanding the universe. This step signifies the emergence of numerical entities, akin to the fundamental constants and quantities in physics that define the properties of the universe. The phrase “God put power into the numbers” symbolizes the idea of the importance of quantifiable information as a fundamental aspect of a universe governed by the laws of quantum mechanics.
Step 3:
Statement: Then, God created 0, the void from which all things emerge. And lo, God had created binary.
Justification: The creation of 0 introduces the concept of nothingness or the void, crucial for defining the absence of quantity. In arithmetic, 0 is the additive identity, meaning any number plus 0 remains unchanged. The combination of 1 (unity) and 0 (void) establishes the binary system, foundational for digital computation and information theory. In quantum mechanics, the binary nature of qubits (0 and 1) underpins quantum computation, where superposition and entanglement emerge from these basic states.
Step 4:
Statement: From the binary, God brought forth 2, which was the first prime number.
Justification: The number 2 is the first and smallest prime number, critical in number theory and the structure of the number system. It signifies the first step into multiplicity and the creation of even numbers. In quantum physics, the concept of pairs (such as particle-antiparticle pairs) and dualities (wave-particle duality) are fundamental, echoing the importance of 2 in establishing complex structures from basic binary foundations.
Step 5:
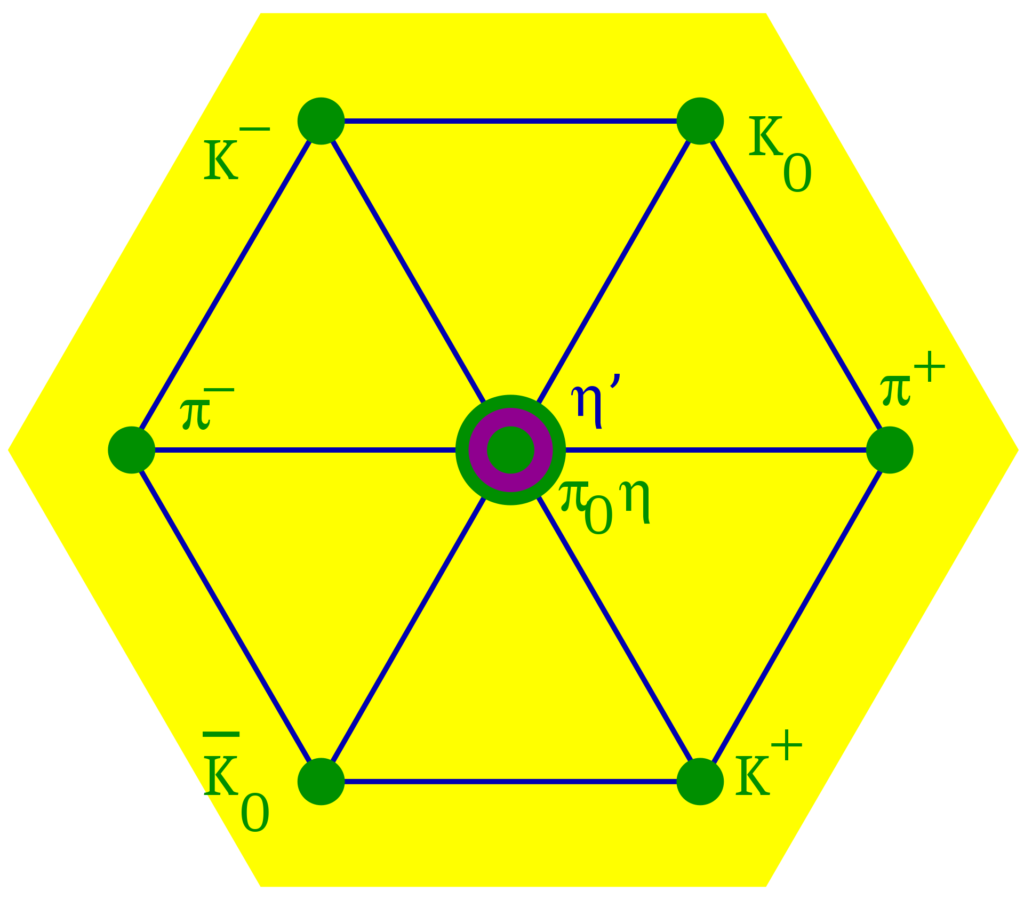
Statement: And then God brought forth 3, which was the second prime number; establishing the ternary, the foundation of multiplicity. God said, “Let 2 bring forth all its multiples,” and so it was. God said, “Let 3 bring forth all its multiples,” and so it was that there were composite numbers. And there were hexagonal structures based on the first composite number 6, which underpinned the new fabric of reality God was creating based on this multiplicity of computation. And there were all the quarks; of which there are 6: up, down, charm, strange, top, and bottom.
Justification: The number 3 is the second prime number and extends the prime sequence, playing a crucial role in number theory. The introduction of 3 establishes ternary structures, which are foundational in various physical phenomena. For example, in quantum chromodynamics, quarks come in three “colors,” forming the basis for the strong force that binds particles in atomic nuclei. The multiples of 2 and 3 cover even numbers and a subset of odd numbers, leading to the formation of composite numbers, analogous to the complex combinations of fundamental particles.
In physics, the arrangement of particles often follows specific symmetries and patterns, like the hexagonal patterns in the quark model representations. The hexagonal symmetry seen in these diagrams represents the symmetrical properties of particles and their interactions, showcasing the deep connection between numerical patterns and physical structures.
Step 6:
Statement: Then God took 6, as multiplied from 2 and 3, and God married 6 to the numbers and subtracted 1. Thus, God created 6n-1 (A), and the first of these was 5, followed by all the other multiples of A, which also includes -1 when n=0. Of these numbers, all of the ones which are A but NOT (6x-1)(6y-1) (which is AA) are prime numbers, and the rest of these are composite numbers of the same form.
Justification: The form 6n−1 (A) generates numbers such as 5, 11, 17, etc., candidates for prime numbers. This step reflects the pattern-seeking nature of mathematics, crucial for identifying primes efficiently. The exclusion of products in this form (AA) ensures the identification of prime numbers, aiding in classifying primes and composites.
Step 7:
Statement: Then, just as God later created Eve from Adam, God inferred B from A by multiplying A’s negative values by -1. Thus, God created 6n+1 (B), the complementary partner to A, mirroring the creation of Eve from Adam’s side. The first of B was 7, followed by all the other multiples of B. The value of B is equal to 1 when n=0, making 1 itself a member of this set. Of these numbers, except for 1, all of the ones which are B but NOT (6x+1)(6y+1) (BB) are prime numbers, and the rest are composite numbers of the same form. And all of the numbers of the form AB, which is (6x-1)(6y+1) were naturally composite, and so none of them were prime.
Justification: The form 6n+1 (B) includes numbers such as 7, 13, 19, etc., which are also prime candidates. By excluding the products of numbers in this form (BB), the narrative ensures an efficient identification of prime numbers. This step reflects the complementary nature of many physical phenomena, such as matter-antimatter pairs. The inclusion of negative values (-A) ensures the number set is symmetric, covering both positive and negative integers, much like the symmetry observed in physical laws and quantum states.
What is the proof in a logical sense that step one is needed?
Logical Proof that Step One is Needed
To provide a logical proof that Step 1 (“Because there was nothing but God, there were no numbers. There was just God. God was 1.”) is necessary, we need to show that all subsequent steps depend fundamentally on the existence of this initial unity (God as 1). Here’s a structured proof using formal logic principles:
Logical Proof
Define the Semiotic Universe:
- Let the Semiotic Universe be the set of all mathematical constructs and entities we are considering.
Assumptions:
- Let ∃1 (Unity, 1) be a fundamental element of the Semiotic Universe, representing the initial condition or God.
- Let ∃N (Numbers, n) be a subset of the Semiotic Universe, representing all numerical entities.
Step 1 (Premise):
- Statement: Because there was nothing but God, there were no numbers. There was just God. God was 1.
- Justification: This step establishes the existence of unity (1) as the foundational entity, from which all numbers and numerical constructs can emerge.
Verification of Dependency on Step 1:
- Step 2: The Creation of Numbers
- Statement: And God said, “Let there be numbers,” and there were numbers.
- Dependency: This step relies on the initial existence of unity (1). Without the concept of 1, the creation of numbers would lack a foundational basis.
- Logical Proof:
- If ¬(∃1), then the concept of numerical entities (N) cannot be defined.
- Therefore, ∃1 exists is a prerequisite for ∃N exists.
- Step 3: The Creation of the Void (0)
- Statement: God created 0, the void from which all things emerge. And lo, He had created binary.
- Dependency: The existence of 0 (the void) is meaningful only if there is an existing concept of unity (1) from which to define absence.
- Logical Proof:
- If ¬(∃1), then 0 cannot be defined as the additive identity.
- Therefore, ∃1 is necessary for the meaningful creation of 0.
- Step 4: The First Prime Number (2)
- Statement: From the binary, God brought forth 2, which was the first prime number.
- Dependency: The number 2 emerges from the binary system, which itself depends on the existence of 1 and 0.
- Logical Proof:
- If ¬(∃1) or ¬(∃0), then the binary system cannot exist, and consequently, 2 cannot be defined.
- Therefore, ∃1 and ∃0 are prerequisites for ∃2.
- Step 5: The Second Prime Number (3) and Multiplication Rules
- Statement: And then God brought forth 3, which was the second prime number; establishing the ternary, the foundation of multiplicity.
- Dependency: The number 3 and the concept of multiplicity rely on the prior existence of 1, 0, and 2.
- Logical Proof:
- If ¬(∃1), ¬(∃0), or ¬(∃2), then the creation of 3 and the ternary system cannot be established.
- Therefore, ∃1 is a fundamental prerequisite.
- Step 6: Creation of 6n-1 (A)
- Statement: God created 6n-1 (A), the first of which was 5. Of these numbers, all that are 6n-1 but NOT (6x-1)(6y-1) (AA) are prime numbers, and the rest are composite.
- Dependency: The form 6n−1 (A) is derived from the existence of 1, 2, and 3.
- Logical Proof:
- If ¬(∃1), ¬(∃2), or ¬(∃3), then the set A={6n−1∣n∈Z} cannot be defined.
- Therefore, ∃1 is necessary.
- Step 7: Creation of 6n+1 (B)
- Statement: God created 6n+1 (B), the first of which was 7. The set B includes all numbers of the form 6n+1, except those that can be factored into the form (6x+1)(6y+1) (BB).
- Dependency: The form 6n+1 (B) also relies on the existence of 1, 2, and 3.
- Logical Proof:
- If ¬(∃1), ¬(∃2), or ¬(∃3), then the set B={6n+1∣n∈Z} cannot be defined.
- Therefore, ∃1 is necessary.
- Completion of the Ternary System
- Statement: The creation of numbers {1,0,−1} establishes the ternary system.
- Dependency: The ternary system relies on the existence of 1 to define the unity, 0 to define the void, and -1 to define the negative unity.
- Logical Proof:
- If ¬(∃1), then neither 0 nor -1 can be meaningfully defined, and the ternary system cannot exist.
- Therefore, ∃1 is a fundamental prerequisite.
Conclusion
- Premise (Step 1): ∃1 (God as Unity).
- Dependency: Each subsequent step relies on the existence of unity (1) as the foundational concept.
- Logical Necessity: Without Step 1 (∃1), the remaining steps cannot logically proceed, as they refer to or manipulate numbers, which would not be defined otherwise.
Therefore, Step 1 is a prerequisite for the logical coherence and execution of the algorithm presented in the narrative. This proof demonstrates that the concept of unity (1) is essential for the creation and differentiation of all numbers and mathematical constructs, and especially if we are to align the story of numbers to the creation narrative of the Bible which gives God preeminence.



